KMP字符串匹配 | Yammer's BLOG

个人感觉，Y总讲的有点抽象，于是上b站看了几个，喵喵的和几个讲的挺好的，但是因为不是c写的代码看不懂(呜呜呜)，所以看来wls的版本就就懂了，代码还是Y总的短。

朴素查询两个长度分别为n，m的字符串的时间复杂度是O(n * m),
而KMP算法只需要O(n + m)，代码很简洁。

当我们需要在长度m的字符串p中，查询具有完整的长度为n的字符串s时，

下面直接开始KMP的操作

我们开始会将两个字符串逐一匹配，直到无法匹配

当发现两个字符无法匹配时，我们如果同时回溯i 和 j 的话就时朴素做法了，但是KMP是保证i不回溯，只回溯j，此时我们发现在两个p的前一段和s已匹配的后一段中有一部分是相同的，如下图

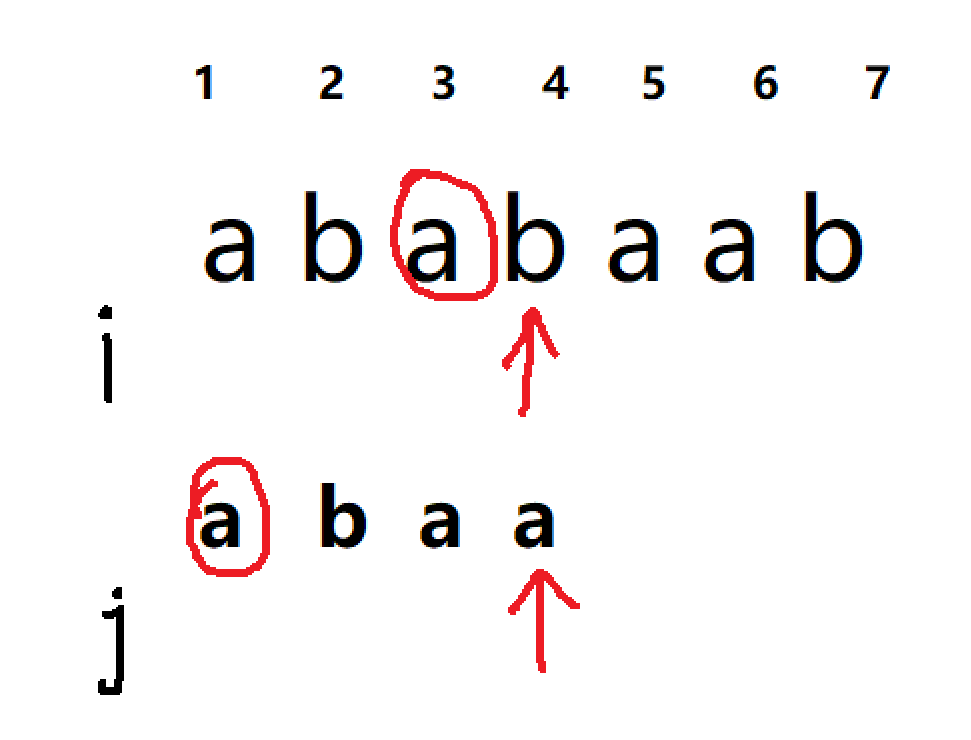
那我们是不是只用将j回溯到1，判断此时p[j + 1] 和 s[i] 是否相等，如果相等的话可以进行下一步操作，如果不相等的话，j还应该继续往前回溯

然后继续匹配，直到 j==n 时说明匹配成功

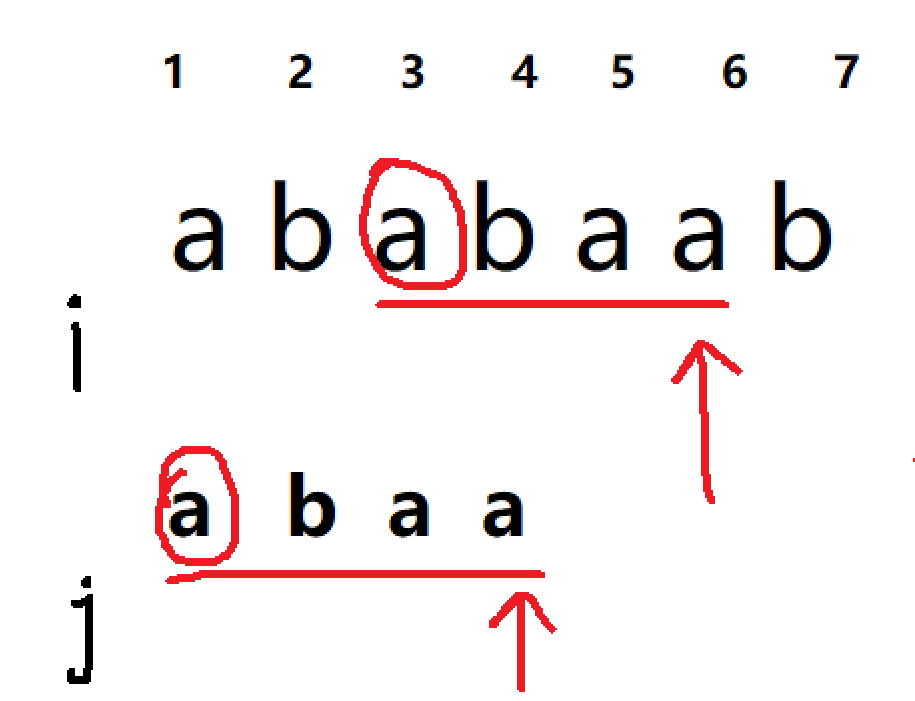
而KMP的重点就是如何进行回溯操作呢，我们发现当寻找s已匹配后缀和p的前缀最大相同时，其实都是对相同的子字符串进行操作，所以我们可以对p字符串查找每个下标对应的前缀长度，这时候我们需要开辟最重要的ne数组。
从上面我们可以了解到，ne数组存的是可回溯长度，也就是前后缀相同的子字符串长度，
但是查询这个也需要O(n * n)暴力查询吗，当然也不需要。(最大相同长度不应该等于整个字符串长度)
对于 i = 1, 我们初始 ne[1] = 0 i = 2, j = 0,
当 p[i] != p[j + 1] 时，我们需要使 j = ne[j] ,使得 j 回溯(j > 0)

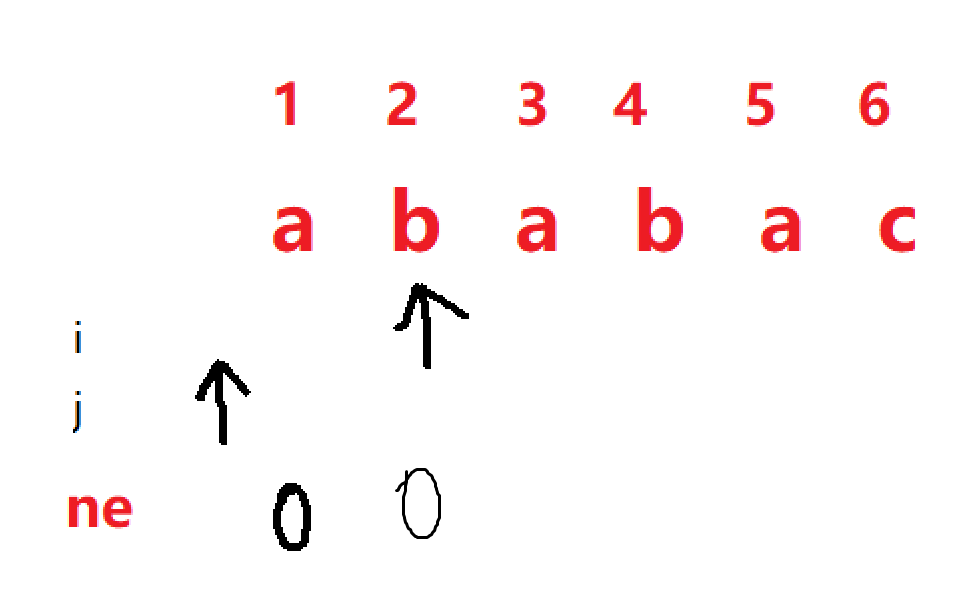
显而易见，当 i == 2 时，ab字符串不存在前后缀相同的子串，所以ne[2] = 0 ，

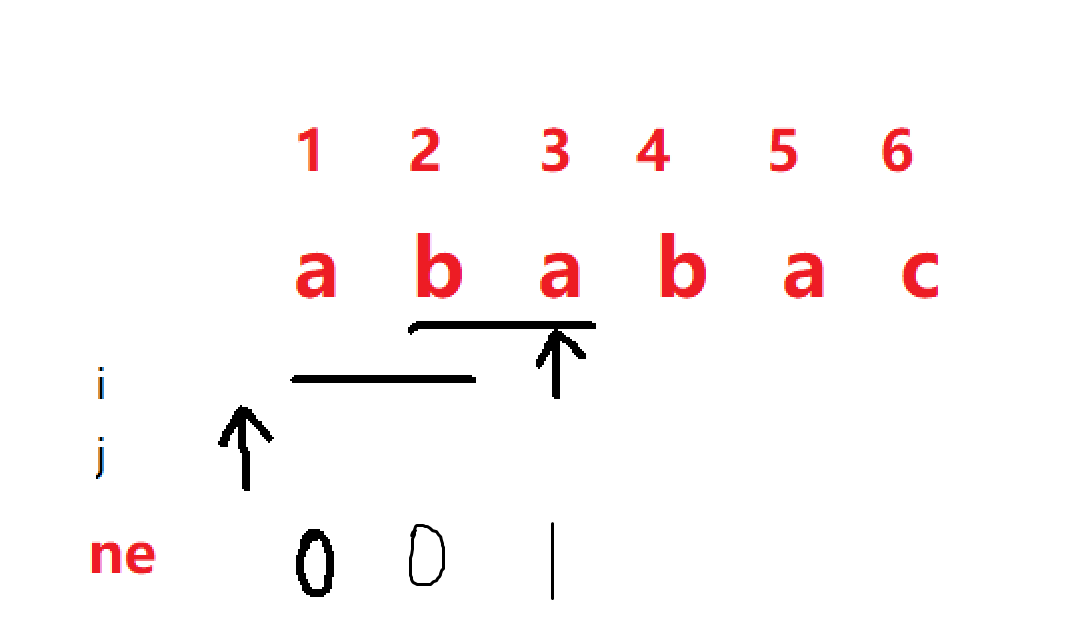
当 i = 3 时，我们发现 p[i] == p[j + 1]，子串aba的最大相同长度是1，所以可以把j后移一位即 j++，然后更新 ne[3] = j = 1,

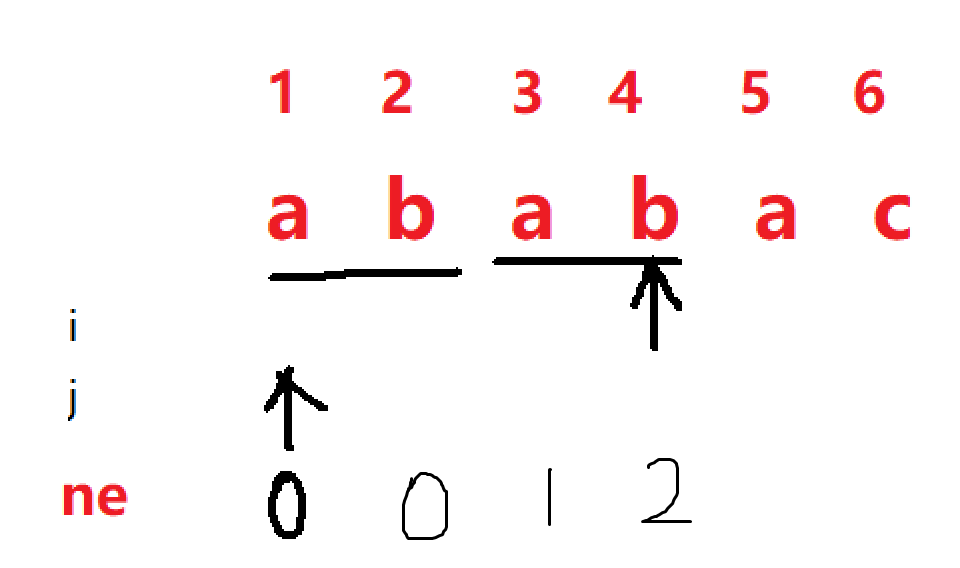
同理，当 i = 4 时，j应该后移一位，ne[4] = 2,

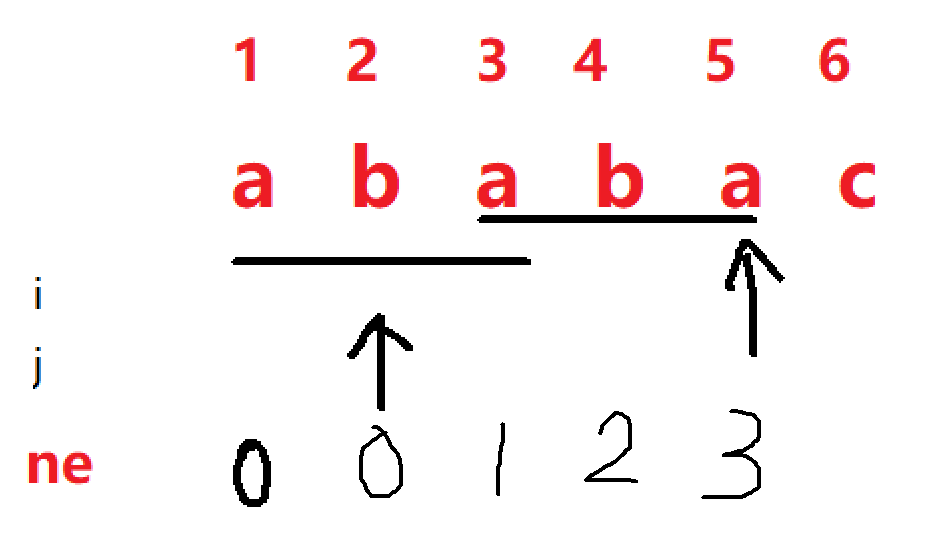
当 i = 5 时， j++，于是 ne[5] = 3,

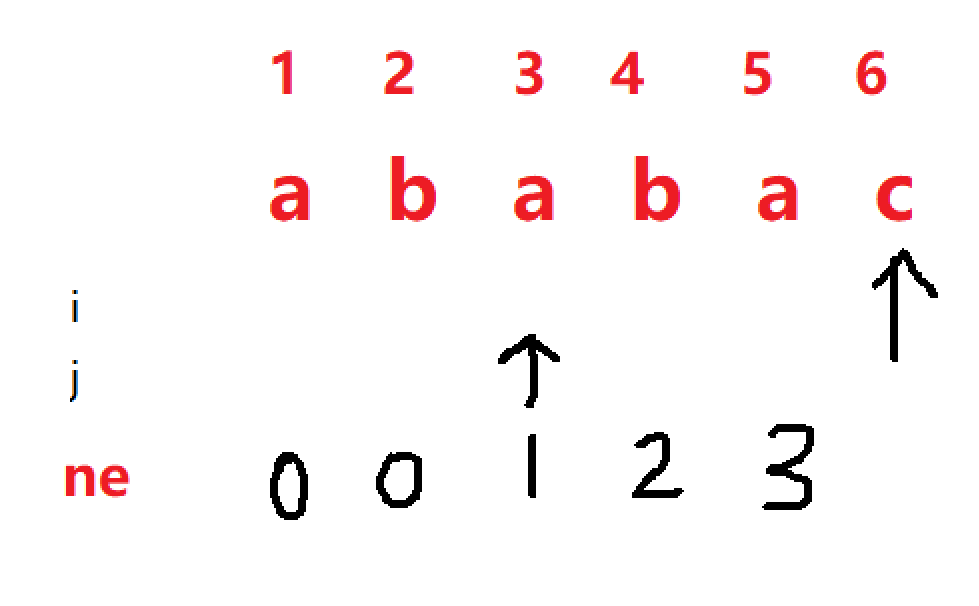
当 i = 6 时，发现 p[i] != p[j + 1] ,于是 j = ne[j] = 1,
然而发现 p[6] != p[1] ,所以继续 j = ne[j] = 0 结束.
因为此时p[i] != p[j + 1] ,所以 j++ 不用执行，ne[6] = 0。
以上ne更新完毕.
对于ne数组的更新，O(n) 的复杂度
我们用代码实现

for(int i = 2, j = 0; i <= n; ++i ){
    while(j && p[i] != p[j + 1])j = ne[j];
    if(p[i] == p[j + 1])j++;
    ne[i] = j;
}

十分简洁，而对于之后的查询相同也是以上类似的做法

for(int i = 1, j = 0; i <= m; ++i){
    while(j && s[i] != p[j + 1])j = ne[j];
    if(p[j + 1] == s[i])j++;
    if(j == n){ 
    //当 p 字符串全部匹配，输出此时s中对应的p字符串的首字母下标
    //然后回溯j   
        cout << i - n + 1 << ' ';
        j = ne[j];
    }
}

KMP洛谷模板题

#include <bits/stdc++.h>
#define rep(i,n,m) for(int i=n;i<=m;++i)
#define per(i,n,m) for(int i=n;i>=m;--i)
#define all(x) x.begin(),x.end()
#define pb(x) push_back(x)
#define PII pair<int,int>
#define VI vector<int>
#define lowbit(x) x&-x
#define INF 1<<30
using namespace std;
typedef long long ll;
const int N=2e5+10;
string s, p;
int ne[N], n, m;
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);
	cin >> s >> p;
	n = p.size();
	m = s.size();
	s = ' ' + s;
	p = ' ' + p;
	VI ans;
	for(int i = 2, j = 0; i <= n; ++i ){
		while(j && p[i] != p[j + 1])j = ne[j];
		if(p[i] == p[j + 1])j++;
		ne[i] = j;
	}
	for(int i = 1, j = 0; i <= m; ++i){
		while(j && s[i] != p[j + 1])j = ne[j];
		if(p[j + 1] == s[i])j++;
		if(j == n){
			cout << i - n + 1 << '\n';
			j = ne[j];
		}
	}
	rep(i, 1, n)cout << ne[i] << ' ';
	return 0;
}

呜呜呜，我要好好学习，不能摆烂