判断二分图
寻找最大匹配
最近学点图论,总不能暑假啥都没学。
所谓二分图,就是对于左右两个集合,每个集合内的任意两点不连边,边只连接两个不同集合内的分别一点,如图(A集合有{1,2,3,4},B集合{1,2,3,4},两个集合的数量和元素都不需要相同)
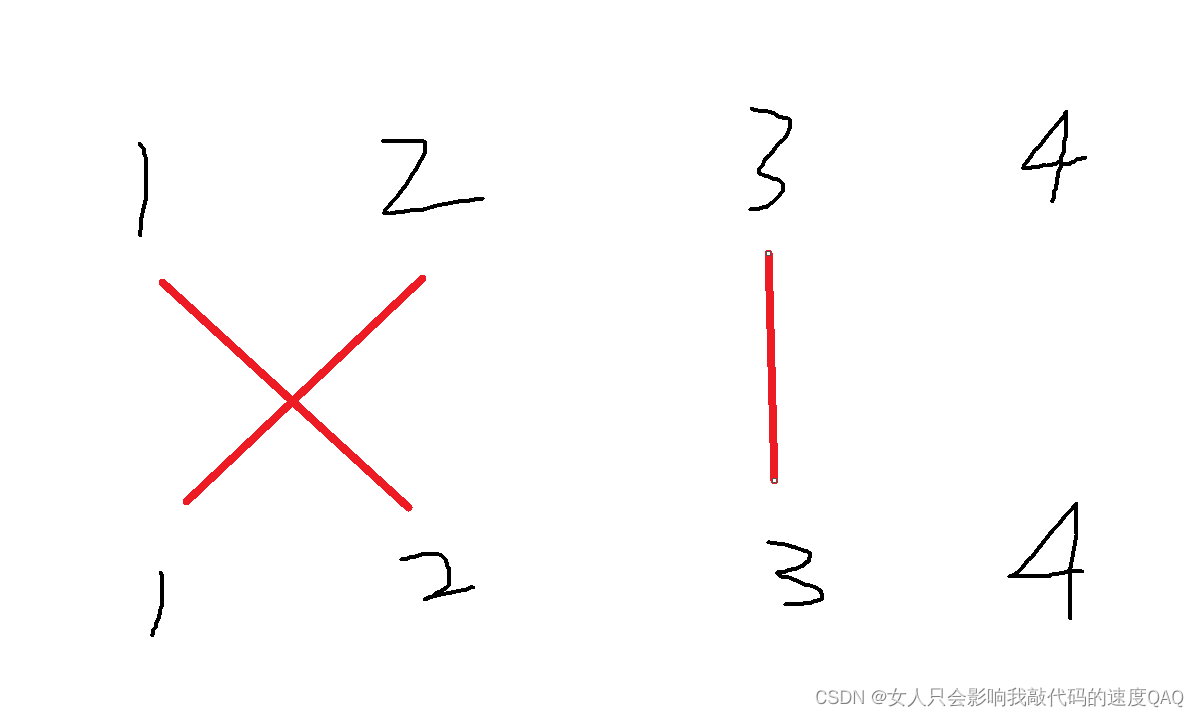
以上的边练成的路径为A(1)→B(2),A(2)→B(1),这是二分图的一种成立条件,即单边无环,但还存在有环的情况,如下
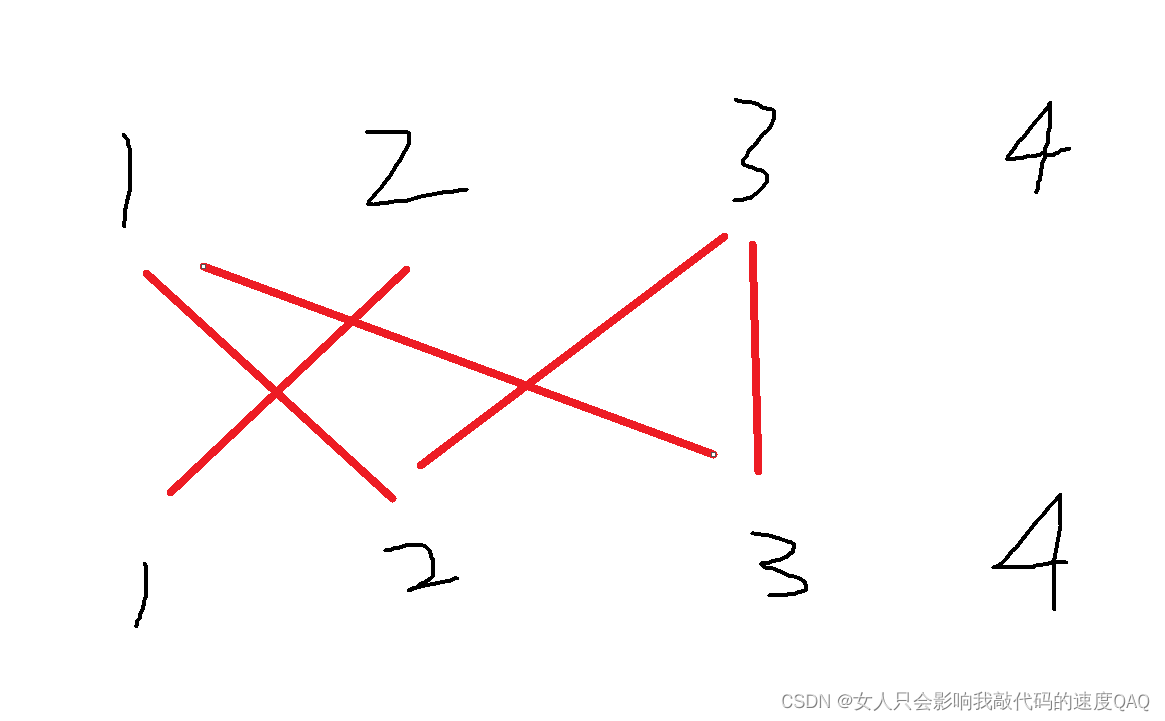
此时的环为A(1)→B(2)→A(3)→B(3)→A(1),此时环内一共有四个元素,可以可以证明的是,若当环内元素为奇数个时,该图必然不为二分图,
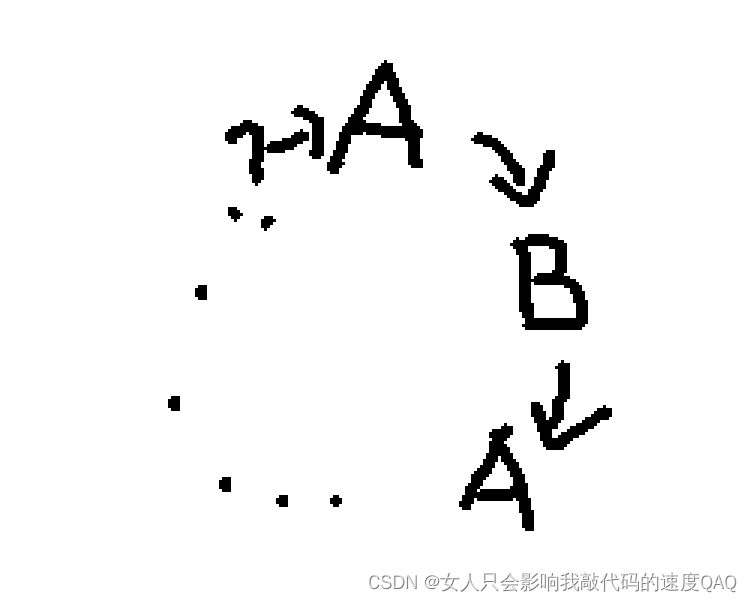
若环内元素有奇数个时,?的位置必然为A,此时A→A与二分图定义矛盾,所以二分图内的环必为偶数环。
对于给定的一个带连边的图,可以用染色法判定二分图,
思路:我们可以把两个不同的集合中的元素染色为1和2。
遍历A中的每一个点,若该点未被染色,则染为1,然后顺着与该点相连的点,将其染为相反的颜色,若过程中发现有下一个点的颜色与当前点的颜色相同,则该图不是二分图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<bits/stdc++.h>
using namespace std;
int const N=2e5+10;
int h[N],ne[N],w[N],cnt=0;
int color[N];
void add(int a,int b){
w[++cnt]=b,ne[cnt]=h[a],h[a]=cnt;
}
bool dfs(int x,int u){
color[x]=u;
for(int i=h[x];i!=-1;i=ne[i]){
int j=w[i];
if(!color[j]){
if(!dfs(j,3-u))return false;
}
else if(color[j]==u)return false;
}
return true;
}
int main()
{
int n,m,k=1;cin>>n>>m;
memset(h,-1,sizeof h);
while (m -- ){
int a,b;cin>>a>>b;
add(a,b);add(b,a);
}
for(int i=1;i<=n;++i){
if(!color[i]){
if(!dfs(i,1)){
k=0;
break;
}
}
}
if(k)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
|
ok,二分图判断完毕,开始匹配问题
上题:
P3386 【模板】二分图最大匹配 - 洛谷 | 计算机科学教育新生态
所谓的匹配:就是在二分图中每个集合的元素只能连一条边,这两个元素的连接就是匹配。
最大匹配:在一个二分图中存在最多的匹配数量
完全匹配:两个集合中的全部元素都能匹配上
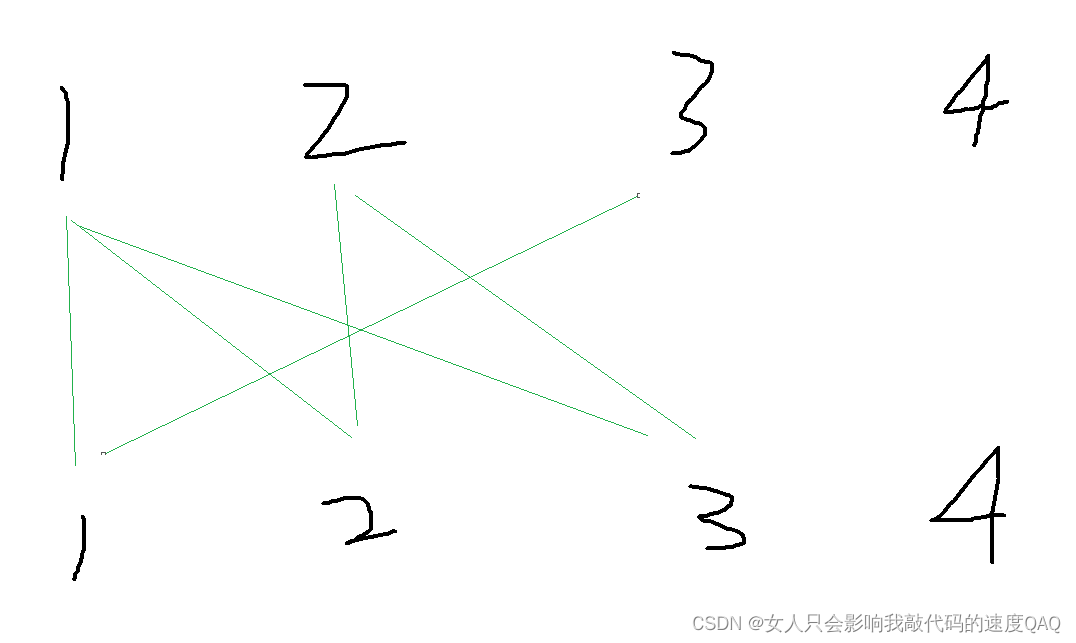
匈牙利算法可以帮助解决这个问题
如图绿线表示两点有连接,按遍历A集合的顺序来,我们先看A中点1,发现A(1)可以与B(2)连,就连这俩
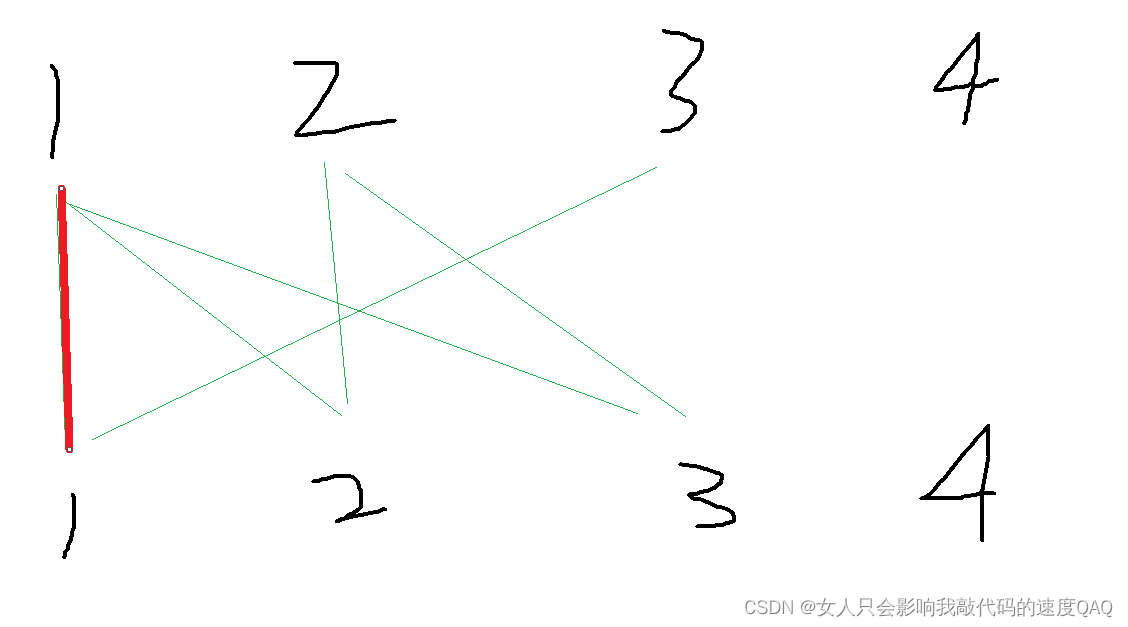
然后看A2的时候发现A2可以和B2连,也就连接他们
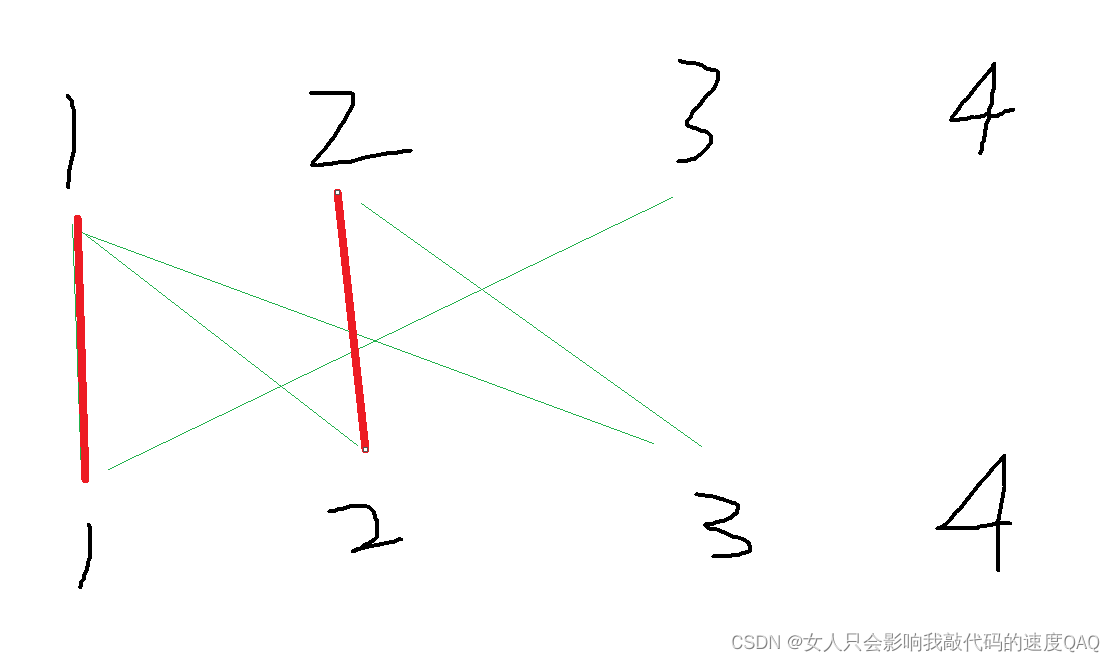
然后到A3的时候,发现A3的第一个连接点B1已经被连了,这就是所谓的增广路了,一点被多个点所连接,这时候我们需要查看B1所连接的点有没有另外的连接点,发现A1还连接着B2,但B2被A2连接了,我们又看A2还另外连B3,而B3没有被连,那么我们就将A2连B3,于是A1就可以连B2,A3可以连B1了,知识点很少,挺容易看懂的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <bits/stdc++.h>
#define rep(i,n,m) for(int i=n;i<=m;++i)
#define per(i,n,m) for(int i=n;i>=m;--i)
#define PII pair<int,int>
#define INF 1<<30
using namespace std;
typedef long long ll;
const int N=2e3+10;
bool link[N][N];
int p[N],st[N],n,m,e,ans=0;
bool dfs(int x){
rep(i,1,m){
if(link[x][i]&&!st[i]){
st[i]=1;
if(p[i]==0||dfs(p[i])){
p[i]=x;
return 1;
}
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);
cin>>n>>m>>e;
while(e--){
int x,y;cin>>x>>y;
link[x][y]=1;
}
rep(i,1,n){
memset(st,0,sizeof st);
if(dfs(i))ans++;
}
cout<<ans;
return 0;
}
|








