线段树入门
发表于：2022-09-07 | 分类： 图论
字数统计: 2.8k | 阅读时长: 14分钟 | 阅读量：

入坑又爱又恨的线段树

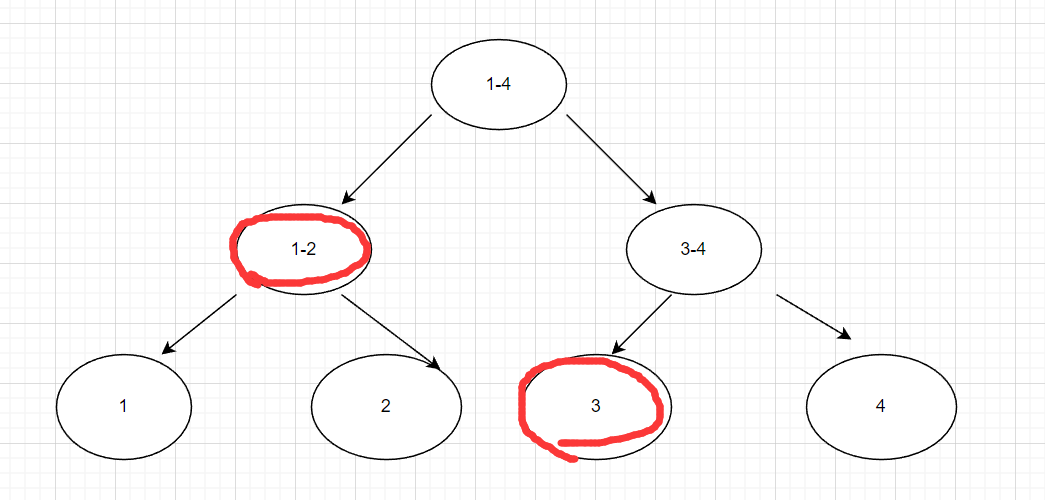
线段树是将一段下标 1-n 的数组划分为一颗二叉搜索树，何为二叉搜索树呢，如下图所示

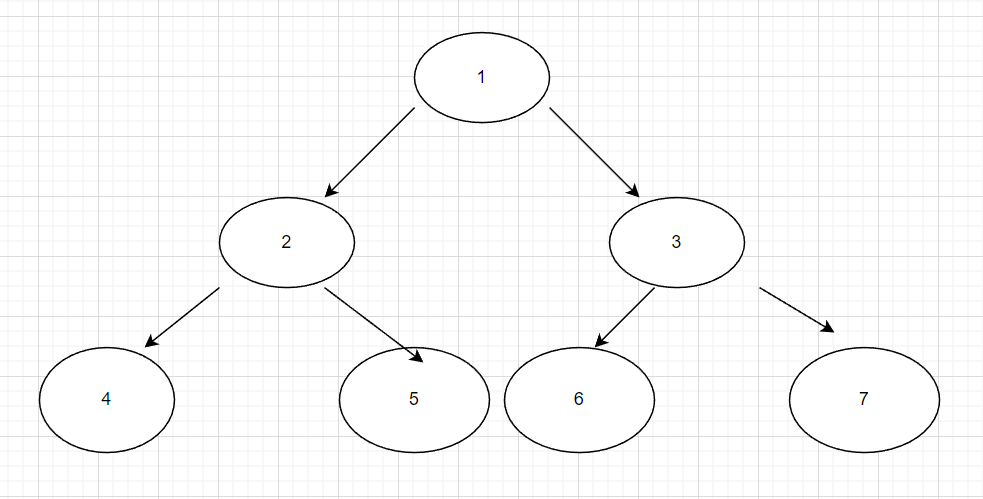
每一个可以继续延申的节点都有两个儿子，
且每一个节点下标k的两个儿子节点的下标分别是k+k和k+k+1，线段是利用这个特性，将1-n的一个区间不断分为两个又两个区间，

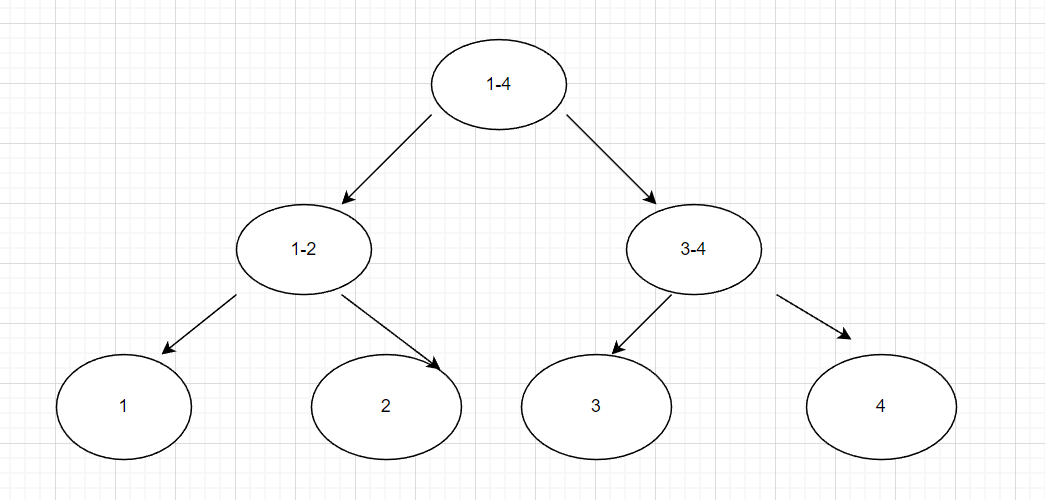
线段树的操作主要分为三个部分

建树(线段树初始化)

插入(对区间进行操作)

查找(获取区间的值)

每次的插入和查找的复杂度均为O(logn)，总复杂度O(nlogn).

不难发现的是，我们可以用每一个节点表示两个儿子的和，从下网上递归得出每一个区间得和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void build(int k, int l, int r) {
	if(l == r) {
		//num是输入的数组值
		f[k] = num[l];
		return; 
	}
	int m=(l+r)>>1;
	//递归左子树
	build(k+k, l, m);

	//递归右子树
	build(k+k+1, m + 1, r); 

	f[k]=f[k+k]+f[k+k+1]; 
	//递归更新
}

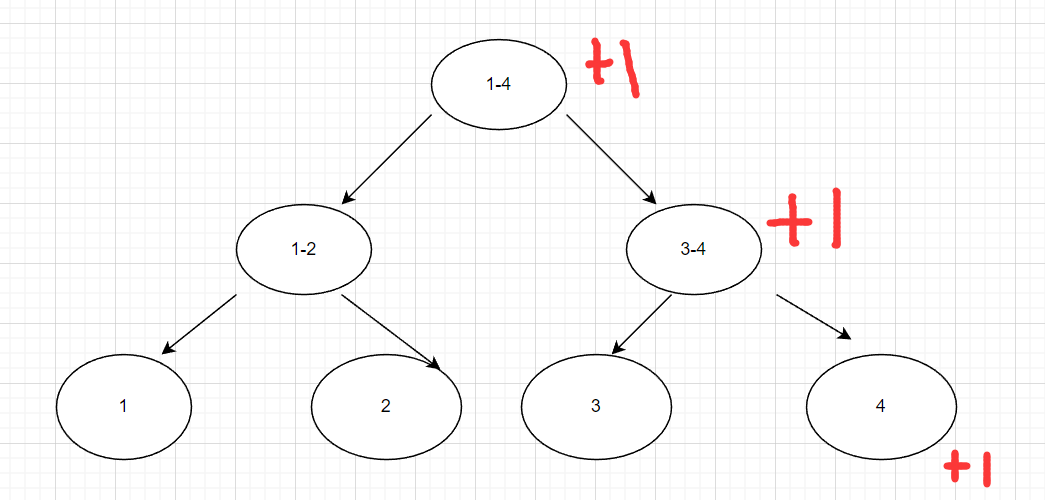
当我们给下标为4的位置+1时，可以发现他的往上的节点都会+1,改递归操作应从上往下进行，
开始发现4∈(1-4)，则(1-4)+1，
然后发现4∈(3-4)，则(3-4)+1，
最后4∈(4)，则(4)+1。

1
2
3
4
5
6
7
8
9
10
11
12
13
void in(int k, int l, int r, int x, int v) {
	f[k]+=v;
	if(l==r) return;
	int m=(l+r)>>1;

	//递归子树
	if(x<=m) 
	    //修改的区间完全在左区间
		in(k+k, l, m, x, val);
	else 
	    //修改的区间完全在右区间
		in(k+k+1, m + 1, r, x, val); 
}

进行区间加值时

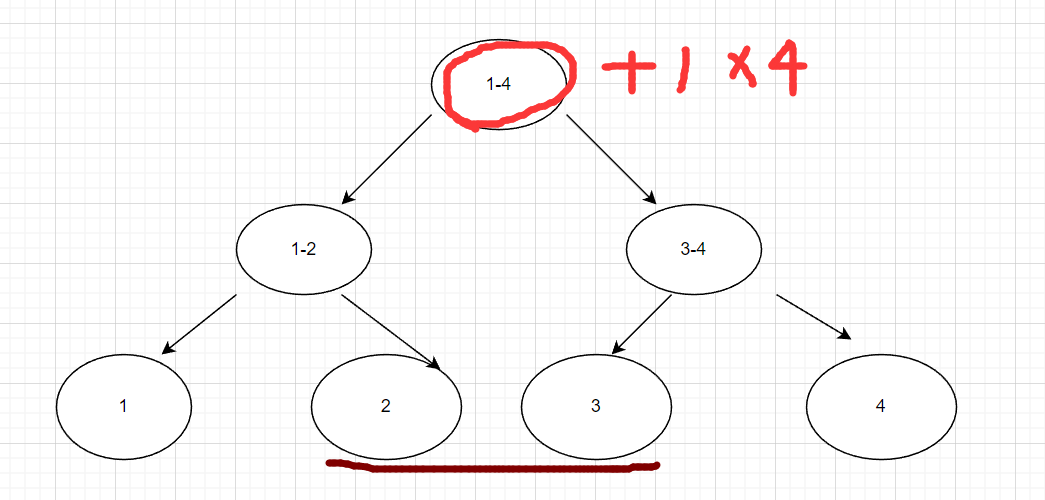
我们可以对这个操作进行优化，当进行区间加值时，如对3-4区间+1
开始发现(3-4)∈(1-4)，则(1-4)+1，
然后发现(3)∈(1-2)，4∈(3-4),则(1-2)+1,(3-4)+1，
最后3∈(3),4∈(4)，则(3)+1,(4)+1。
在我们对区间进行范围性加法运算的时候，需要用个数组对节点下标进行标记，表示加法运算到该节点结束

要注意的是

我们使用标记是使得所有包含更改区间的节点都能更新值，且到完全覆盖修改区间的时候标记不下传
刚开始我想过，能不能不用 标记，直接包含的每段区间都 f[k]+=(y-x+1)*t; 就好了，结果是不行的，
如果不用标记，我修改了(1-4)的值+1，会在第一个节点停止，当我查询(2-3)的时候，会一直递归找到(2),(3)的值，发现并不能获取更新后的值，所以需要标记来记录更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void in(int k,int l,int r,int x,int y,ll t){
  //当前节点为k，lr为节点的区间范围，xy为所要修改的区间范围，t为要加的值
	if(l==x&&r==y){  //范围符合，v数组进行标记
		v[k]+=t;	
		return ;
	}
  //继续寻找
	f[k]+=(y-x+1)*t;   //对属于范围内的元素进行加法运算
	int m=(l+r)>>1; 
  //将区间一分为二
	if(y<=m)  
	    in(k+k,l,m,x,y,t);
     //查询区间右边界<=当前区间左儿子右边界，
     //查询区间∈当前区间左儿子
	else  
	if(x>m)
	   in(k+k+1,m+1,r,x,y,t);
     //查询区间左边界>=当前区间右儿子左边界，
     //查询区间∈当前区间右儿子
	else 
	    in(k+k+1,m+1,r,m+1,y,t),in(k+k,l,m,x,m,t);
       //否则递归两边区间
}

至此我们便可以对区间进行范围性加法操作，
但要如何查询呢
当我们要查询1-3的区间和时，
发现(1-3)不完全∈(1-4)，却可以发现其儿子(1-2),(3-4)中，都包含了查询区间，于是把查询区间分为两块，分别对(1-2),(3-4)进行查询(1-2),(3)
接着我们发现(1-2)∈(1-2),则返回答案，
(3)不完全∈(3-4),发现其左儿子包含了3，则递归左儿子，然后查询到了(3)，便返回(3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
ll cal(int k,int l,int r,int a,int b,ll ans){
  //ans记录当前节点接受的值
	ans += v[k];
  //累计已标记的值
	if(l==a&&r==b){
		return 1LL*(f[k] + ans * (b - a + 1 ));
    //刚好查询到范围，返回当前区间和+标记值*区间范围
	}
	int m=(l+r)>>1;
	if(b<=m)return cal(k+k,l,m,a,b,ans);
       //查询区间右边界<=当前区间左儿子右边界，
      //查询区间∈当前区间左儿子
	else if(a>m)return cal(k+k+1,m+1,r,a,b,ans);
       //查询区间左边界>=当前区间右儿子左边界，
      //查询区间∈当前区间右儿子
	else 
	return cal(k+k,l,m,a,m,ans)+cal(k+k+1,m+1,r,m+1,b,ans);
         //否则递归两边区间
}

另外对于n个数的数组，把他递归分成一颗二叉搜索树，其的数组范围就是结点的数量，应该开到4n
洛谷原题1线段树加法
answer code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
#define rep(i,n,m) for(int i=n;i<=m;++i)
#define per(i,n,m) for(int i=n;i>=m;--i)
#define PII pair<int,int>
#define lowbit(x) x&-x
#define INF 1<<30
using namespace std;
typedef long long ll;
const int N=4e5+10;
int num[N];
ll f[N],v[N];
void build(int k,int l,int r){
	v[k]=0;
	if(l==r){
		f[k]=num[l];
		return ;
	}
	int m=(l+r)>>1;
	build(k+k,l,m);
	build(k+k+1,m+1,r);
	f[k]=f[k+1+k]+f[k+k];
}
void in(int k,int l,int r,int x,int y,ll t){
	if(l==x&&r==y){
		v[k]+=t;	
		return ;
	}
	f[k]+=(y-x+1)*t;
	int m=(l+r)>>1;
	if(y<=m)
	    in(k+k,l,m,x,y,t);
	else  
	if(x>m)
	   in(k+k+1,m+1,r,x,y,t);
	else 
	    in(k+k+1,m+1,r,m+1,y,t),in(k+k,l,m,x,m,t);

}
ll cal(int k,int l,int r,int a,int b,ll ans){
	ans += v[k];
	if(l==a&&r==b){
		return 1LL*(f[k] + ans * (b - a + 1 ));
	}
	int m=(l+r)>>1;
	if(b<=m)return cal(k+k,l,m,a,b,ans);
	else if(a>m)return cal(k+k+1,m+1,r,a,b,ans);
	else 
	return cal(k+k,l,m,a,m,ans)+cal(k+k+1,m+1,r,m+1,b,ans);
}
int main()
{
	int n,m;cin>>n>>m;
	rep(i,1,n)cin>>num[i];
	build(1,1,n);
	while(m--){
		int t;cin>>t;
		if(t==1){
			int a,b;ll c;cin>>a>>b>>c;
			in(1,1,n,a,b,c);
		}
		else {
			int b,c;cin>>b>>c;
			cout<<cal(1,1,n,b,c,0)<<endl;
	    }
	}
	return 0;
}

🥰🥰🥰😘
2022-9-7 23：24
待更新区间乘法…

太难啦太难啦，为什莫这么烦 QAQ
洛谷原题2线段树乘法

当我们需要对区间进行乘法操作和加法时，一个标记肯定不满足，所以需要另开一个数组标记该结点需要的乘数，并且这两种操作方法对于取模操作是不封闭的，每一次都可以取模运算。

此外我们需要用一个函数来维护区间内的标记，使得标记下传，对于题目给的加法和乘法操作，在下传标记的时候要么先加后乘，要么先乘后加，而我们采用的是先乘后加。（）

//push维护标记下传

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void push(int k,int l,int r){
    int m=(l+r)>>1;
	//维护节点权值
	//f[儿子]=(mul[父亲]*f[儿子]+add[父亲]*(区间长度))%模
    f[k+k]=(mul[k]*f[k+k]+add[k]*(m-l+1))%p;
    f[k+k+1]=(mul[k]*f[k+k+1]+add[k]*(r-m))%p;
    
	//维护乘法和加法后的值
    //mul[儿子]=(mul[父亲]*mul[儿子])%模
	mul[k+k]=(mul[k]*mul[k+k])%p;
    mul[k+k+1]=(mul[k]*mul[k+k+1])%p;

    //add[儿子]=(add[儿子]*mul[父亲]+add[父亲])%模
    add[k+k]=(add[k+k]*mul[k]+add[k])%p;
    add[k+k+1]=(add[k+k+1]*mul[k]+add[k])%p;
    
	//初始化标记
    mul[k]=1;
    add[k]=0;
    return ;
}

为了使得标记值每次都能往下传递，所以每次操作都应该用一次push
来保证标记传递和标记初始化
区间乘法，t表示乘上的数

1
2
3
f[k]=(f[k]*t)%p;
mul[k]=(mul[k]*t)%p;
add[k]=(add[k]*t)%p;

区间加法

1
2
add[k]=(add[k]+t)%p;
f[k]=(f[k]+t*(r-l+1))%p;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <bits/stdc++.h>
#define rep(i,n,m) for(int i=n;i<=m;++i)
#define per(i,n,m) for(int i=n;i>=m;--i)
#define PII pair<int,int>
#define lowbit(x) x&-x
#define INF 1<<30
using namespace std;
typedef long long ll;
const int N=3e5+10;
ll num[N],f[N],add[N],mul[N],p;
void build(int k,int l,int r){
	add[k]=0;
    mul[k]=1;
	if(l==r){
		f[k]=num[l];
        f[k]%=p;
		return ;
	}
	int m=(l+r)>>1;
	build(k+k,l,m);
	build(k+k+1,m+1,r);
	f[k]=(f[k+1+k]+f[k+k])%p;
    //cout<<k<<' '<<f[k]<<endl;
}
void push(int k,int l,int r){
    int m=(l+r)>>1;
    f[k+k]=(mul[k]*f[k+k]+add[k]*(m-l+1))%p;
    f[k+k+1]=(mul[k]*f[k+k+1]+add[k]*(r-m))%p;
    //维护乘法和加法后的值
    mul[k+k]=(mul[k]*mul[k+k])%p;
    mul[k+k+1]=(mul[k]*mul[k+k+1])%p;

    add[k+k]=(add[k+k]*mul[k]+add[k])%p;
    add[k+k+1]=(add[k+k+1]*mul[k]+add[k])%p;
    //维护乘法加法的值
    mul[k]=1;
    add[k]=0;
    //初始化
    return ;
}
//乘法操作
void in1(int k,int l,int r,int x,int y,ll t){
    if(y<l||x>r) return ;

    if(x<=l&r<=y){
        f[k]=(f[k]*t)%p;
        mul[k]=(mul[k]*t)%p;
        add[k]=(add[k]*t)%p;
        return ;
    }

    push(k,l,r);
    int m=(l+r)>>1;
    in1(k+k,l,m,x,y,t);
    in1(k+k+1,m+1,r,x,y,t);
    f[k]=(f[k+k+1]+f[k+k])%p;
    return ;
}
//加法操作
void in2(int k,int l,int r,int x,int y,ll t){
    if(y<l||x>r) return ;

    if(x<=l&&r<=y){
        add[k]=(add[k]+t)%p;
        f[k]=(f[k]+t*(r-l+1))%p;
        return ;
    }

    push(k,l,r);
    int m=(l+r)>>1;
    in2(k+k,l,m,x,y,t);
    in2(k+k+1,m+1,r,x,y,t);
    f[k]=(f[k+k+1]+f[k+k])%p;
    return ;
}
//计算区间和
ll cal(int k,int l,int r,int a,int b){
    if(b<l||a>r) return 0;

    if(a<=l&&r<=b){
        return f[k];
    }

    push(k,l,r);
    int m=(l+r)>>1;
    return (cal(k+k,l,m,a,b)+cal(k+k+1,m+1,r,a,b))%p;
}
int main()
{
	int n,m;cin>>n>>m>>p;
	rep(i,1,n)cin>>num[i];
	build(1,1,n);
	while(m--){
		int t;cin>>t;
		if(t==1){
			int a,b;ll c;cin>>a>>b>>c;
			in1(1,1,n,a,b,c);
		}else if(t==2){
            int a,b;ll c;cin>>a>>b>>c;
            in2(1,1,n,a,b,c);
        }
		else {
			int b,c;cin>>b>>c;
			cout<<cal(1,1,n,b,c)<<endl;
	    }
	}
	return 0;
}

差不多吧，总觉得还是有个点不是很透彻，慢慢悟吧
2022-9-8 19：54

微博摸张长图

区间操作 二叉搜索树
上一篇:
codeforces135D
下一篇:
树状数组入门

    • Copyright © 2019 - 2020 yuang01 | Powered by Hexo | Theme Bamboo