Lut本科回忆录

$Y_{lq}$

洛谷割点模板

何为割点？
简单来说是在一个无向图中，若删除该点，则该无向图将会被分为两部分

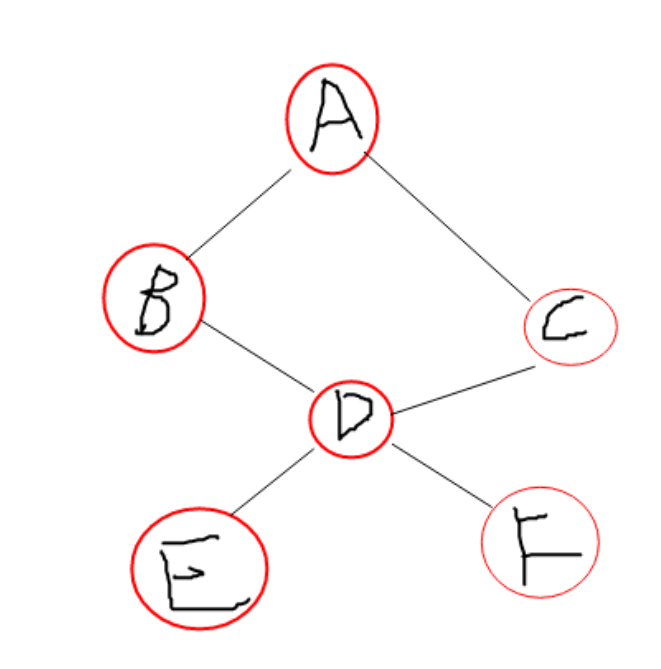
如上图所示，结点$D$是一个割点，但是$A、B、C、E、F$不是割点

此外在这里我们引入$dfn[i],low[i]$ 两个概念
$dfn[i]:遍历到该结点$$i$$时的时间，称之为——时间戳$
$low[i]:不通过父结点$$i$$所能到达的最小的时间戳的值，即最小回溯值$
例如对上图我们从$A$结点开始遍历，标记时间戳是这样的

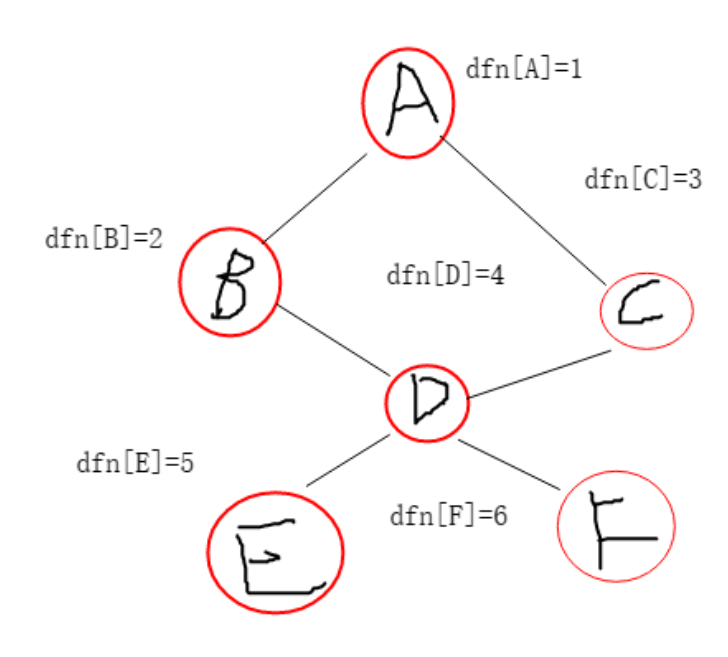
再之，我们求得每个结点的$low$值如下

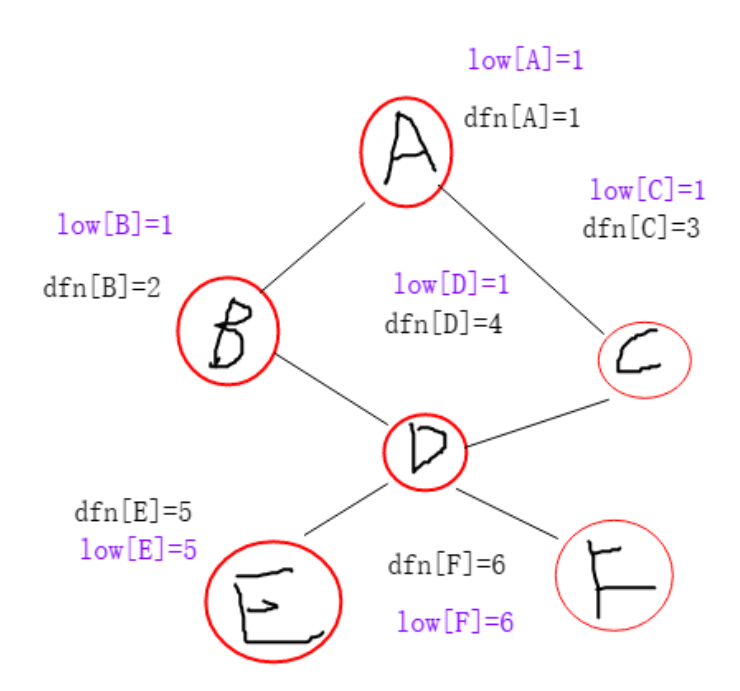
我们可以发现，对结点$E、F$而言，他们无法回溯到比自己更小的$dfn$值，即显然他们的父节点$D$为一个割点。
我们用$O(n)$的复杂度遍历图中的每一个结点，并对其的$dfn、low、st$进行初始化

st[u] = 1;
dfn[u] = low[u] = ++ in;
//我们以一个全局变量in来表示记录到该节点的时间

结点为割点的两种情况：
1、当前结点$u$为根结点，且存在两个以上的子结点
2、当前结点$u$不为根节点，且对于其连接的子结点$v$而言，$low[v]>=dfn[u]$，说明其儿子$v$无法通过其他结点跑到$u$结点之前
因此，当我们遍历发现该结点为标记过时

if(!st[v]){
    num ++; //累计结点u的子结点数量
    tarjan(v, u); //遍历v结点出发的图
    low[u] = min(low[u], low[v]); //更新low[u]
    if(fa != u && low[v] >= dfn[u] && !ok[u]){  //倘若该节点不是根节点，且满足割点条件
        ok[u] = 1;
        ans ++;
    }
}

反之该结点标记过了，并且结点没有往回跑的话，我们如果继续用$low[u]=min(low[u],low[v])$的话，
以下图为例，

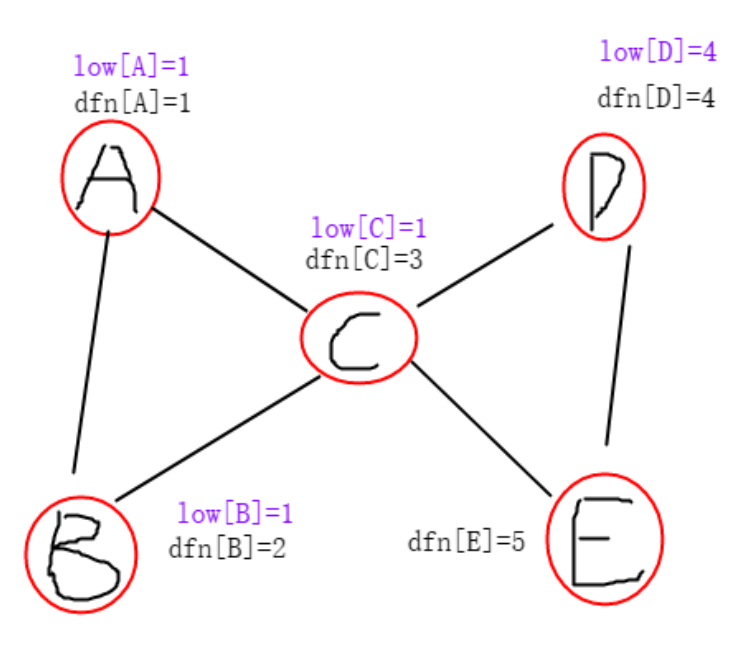
当我们在从$D$跑到$E$时，如果对$E$用$low[E]=min(low[E],low[C])$的话，那么$low[E]=low[C]=1$，此时不满足显然的割点条件，因此
我们需要对标记过的连接值取$low[u]=min(low[u],dfn[v])$
至此我们得出该题的解决方案.

代码

#include "bits/stdc++.h"
#define rep(i, n, m) for(int i = n; i <= m; ++i)
using namespace std;
const int N = 8e5 + 10;
int dfn[N], low[N], st[N], ok[N], in = 0;
int h[N], ne[N], e[N], cnt, ans = 0;
void add(int a, int b){
     e[cnt] = b, ne[cnt] = h[a], h[a] = cnt++;
}
void tarjan(int u, int fa){
    st[u] = 1;
    dfn[u] = low[u] = ++ in;
    int num = 0;
    for(int i = h[u]; ~i; i = ne[i]){
        int v = e[i];
        if(!st[v]){
            num ++;
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(fa != u && low[v] >= dfn[u] && !ok[u]){
                ok[u] = 1;
                ans ++;
            }
        }else if(v != fa){
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(u == fa && num >= 2 && !ok[u]){
        ok[u] = 1;
        ans ++;
    }
}
int main()
{
    //ios::sync_with_stdio(0); cin.tie(0);
    memset(h, -1, sizeof h);
    memset(ok, 0, sizeof ok);
    int n, m; cin >> n >> m;
    rep(i, 1, m){
        int u, v; cin >> u >> v;
        add(u, v), add(v, u);
    }
    rep(i, 1, n){
        if(!st[i]){
            in = 0;
            tarjan(i, i);
        }
    }
    cout << ans << '\n';
    rep(i, 1, n){
        if(ok[i]) cout << i << ' ';
    }
    return 0;
}