快速幂应用的推广
ab
来简单复习一下快速幂
对于一个要求计算 的题目, ,若用朴素算法的复杂度是O(b)
1
2
3
4
| int ans = a;
for(int i = 1; i <= b; ++i){
ans = ans * a;
}
|
但倘若我们能让b二进制分解的话,可以优化该复杂度
假设当b = 8时,b的二进制表示是 1000,即可以表示为
1
2
3
4
5
6
| int ans = 1;
while(b){
a *= a;
b >>= 1;
}
ans = ans * a;
|
因此我们只需计算b二进制表达式下的每一个1到答案即可
1
2
3
4
5
6
7
8
9
| int qm(int a, int b){
int ans = 1;
while(b){
if(b & 1) ans *= a;
a *= a;
b >>= 1;
}
return ans;
}
|
在取模p的情况下
1
2
3
4
5
6
7
8
9
| int qm(int a, int b, int p){
int ans = 1;
while(b){
if(b & 1) ans = ans * a % p;
a = a * a % p;
b >>= 1;
}
return ans;
}
|
那么快速幂除了做简单的数的幂次,还能干些啥呢?
对于一个 Fibonacci 数列,我们知道它的递推公式
但是对于,其O(n)的复杂度也是很大的,
我们可以发现这个其实可以用矩阵表示
此时我们就可以用快速幂计算这个矩阵,把复杂度从O(n)降低到O(logn)
举个例题:
对于前 n 项斐波那契数列
我们知道,
我们移项使得 ,
也就是
然后我们将n项列出来,
我们将所有式子累加
所以我们可以用快速幂计算出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <bits/stdc++.h>
#define rep(i,n,m) for(int i=n;i<=m;++i)
#define int long long
using namespace std;
int ans[2] = {1, 0};
int A[2][2] = {
{1, 1},
{1, 0}
};
int n, p;
void mul(int a[], int b[][2]){
int c[2] = {0};
c[0] = a[0] * b[0][0] + a[1] * b[0][1];
c[1] = a[0] * b[1][0] + a[1] * b[1][1];
a[0] = c[0] % p;
a[1] = c[1] % p;
}
void cal(int a[][2], int b[][2]){
int c[2][2] = {0};
rep(i, 0, 1){
rep(j, 0, 1){
rep(k, 0, 1){
c[i][j] += a[i][k] * b[k][j] % p;
}
}
}
rep(i, 0, 1){
rep(j, 0, 1){
a[i][j] = c[i][j] % p;
}
}
}
signed main()
{
cin >> n >> p;
n += 2;
if(p == 1){
cout << 0;
return 0;
}
while(n){
if(n & 1) mul(ans, A);
cal(A, A);
n >>= 1;
}
printf("%lld", ans[1] - 1);
return 0;
}
|
快速幂最常用的是还可以用来求逆元,由费马小定理得:
当b, m满足互质时,且 a 可以整除 b,
使得
得证:
对 a % p != 0 时
a % p 的逆元为
即可以用快速幂 求得。
在b站up主视频结尾看到这样的一个思考题
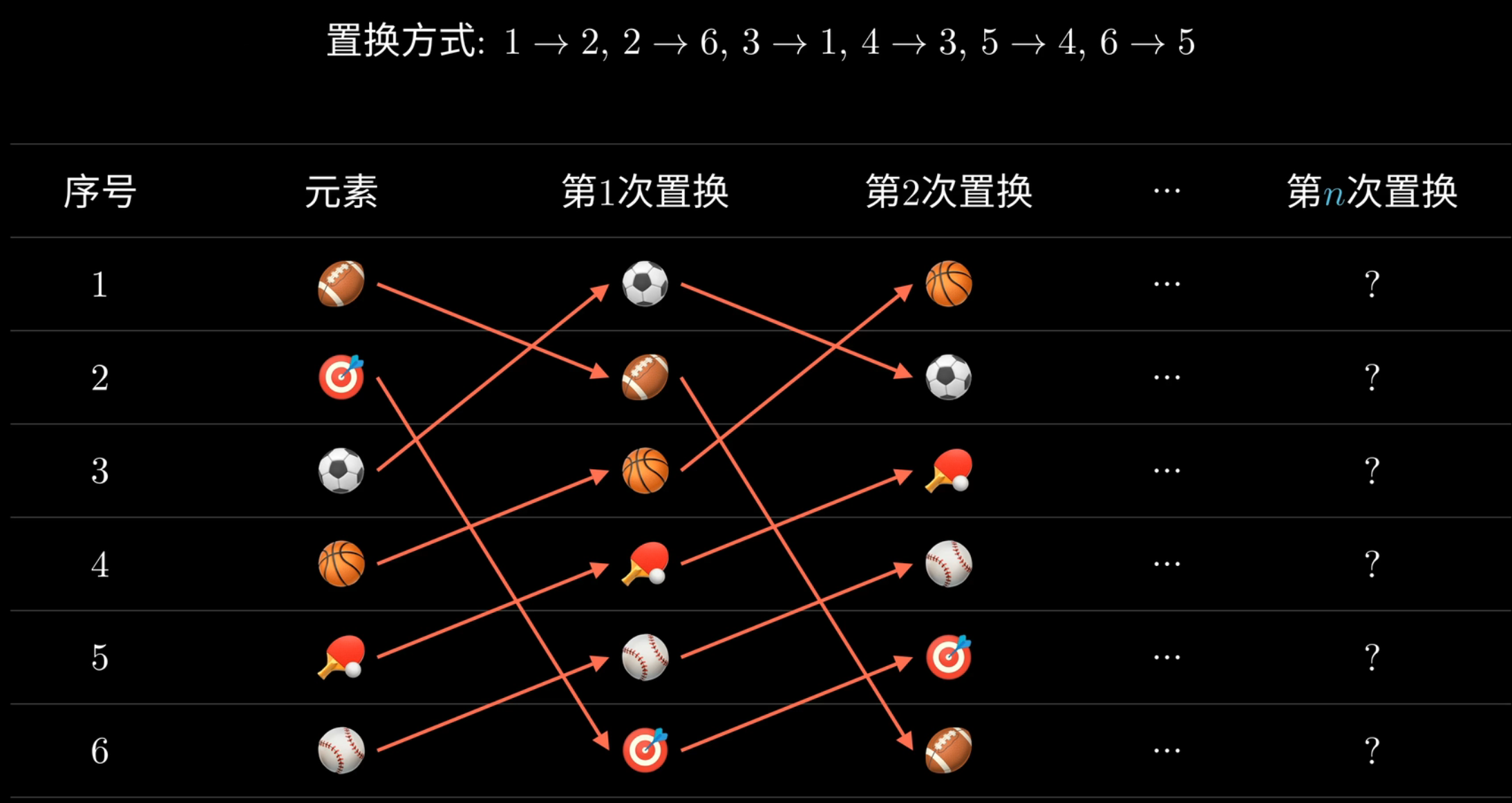
可以先自己思考一下
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
我们不妨把每种元素看成一个数,然后转换成一个列矩阵
对于第一次变换,我们可以给其左乘以一个 6 * 6 的方阵
于是
我们可以发现每一次置换就是左乘一个方阵,所以对于 n 次置换,那么答案就是
可以用快速幂求得。
这是前几天拍的月全食,红色已经过去了