Lut本科回忆录

堆优化的dijkstra板子*

对于单源最短路的问题，目前已知最快的解决算法就是堆优化处理过的dijkstra（条件当然是不存在负边的情况下，若存在负边的情况则要用spfa辽，但是蒻苟不会嘻嘻🤭）

dijkstra的本质是贪心，对于求目标两个位置间的最短权边和，查找从起点位置到每个点的最短距离，同时更新与该当前点相关的点的距离。

这种存图方式只需要开一个数组存储每个点引出的第一条边，然后存储每个点作为起点的每条边，这样就可以做到不重不漏。

在链式前向星存图中，我们需要定义一个结构体：

struct EDGE 
{
    int next;
    int to;
}edge[1000000];

和一个数组

int head[1000000];

和一个变量：

int cnt=0;//指针

你会发现竟然没存起点！！其实起点是用headhead存的

举例：

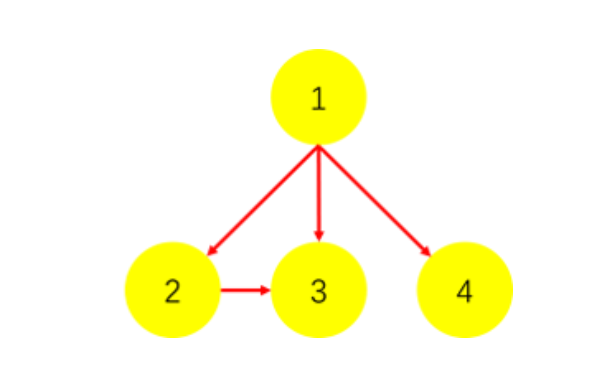
如图：这样的一个有向图，输入是：

1 2
1 3
1 4
2 3

逐步分析：
1.输入1 2，代表1连向2。

cnt++;//作为结构体下标，没有意义
head[1]=cnt;//结点1的第一个儿子存在了edge[cnt]里面
edge[cnt].to=2;结点1的儿子是2

此时： cnt=1

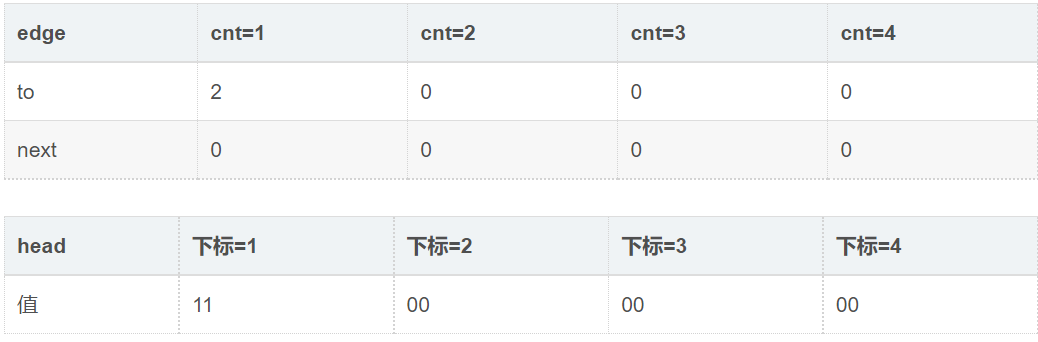
2.输入1 3，代表1连向3。

cnt++;
head[1]=cnt;
edge[cnt].to=3;结点1的儿子是3
//这时,3成为了结点1的儿子，不过2被挤了下去...
//所以要引入结构体中next元素，记录：3还有个兄弟（next）是2
//所以代码要换成：
cnt++;
edge[cnt].to=3;//结点1连向3
edge[cnt].next=head[1];//3的兄弟是2
head[1]=cnt;//更新head

此时： cnt=2

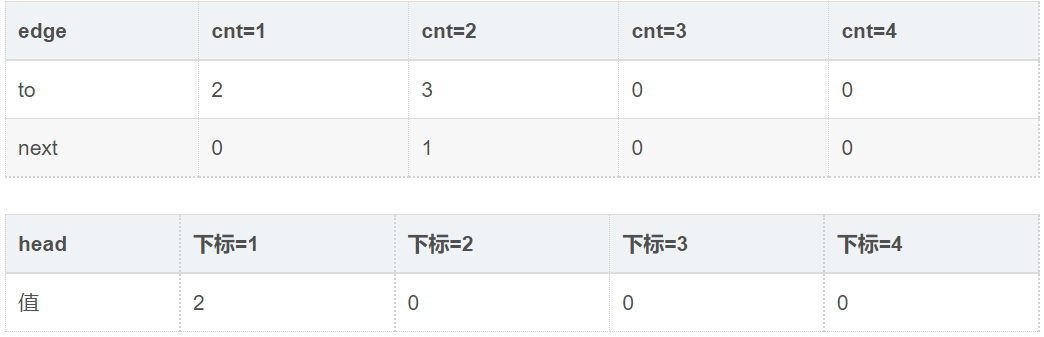
3.输入1 4，代表1连向4。
此时cnt=3

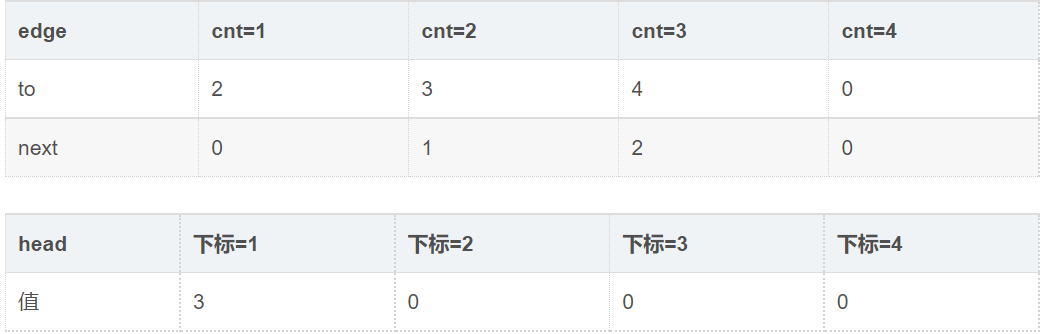
4.输入2 3，代表2连向3。

此时： cnt=4

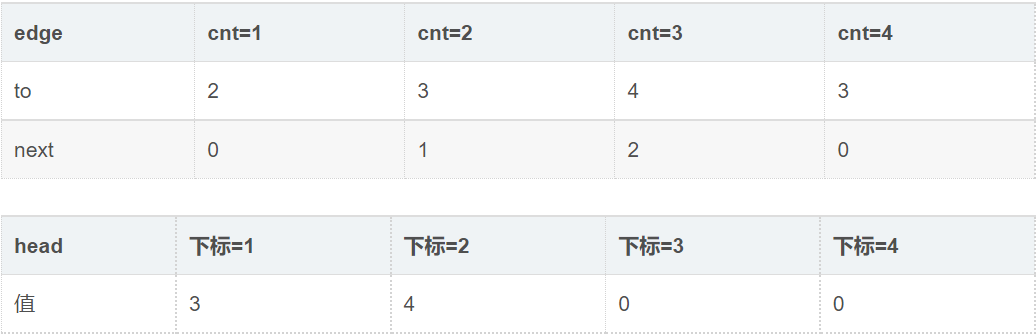
可以理解的是，next存的是当前结点连接的最近的兄弟结点的下标，如1->2，1->3，1->4，则4的next是3，3的next是2。

而head 存的是当前结点指向的最远的结点的下标，1->2，1->3，则head [1] =3，

对于带权值的问题，在结构体中加入一个元素记录权值即可

代码：(带权值）

#include<iostream>
using namespace std;
struct edge 
{ 
    int next;
    int to;
    int wei;
}edge[MAXM];
int head[MAXN];//head[i]为i点的第一条边
int cnt=0;
void addedge(int u,int v,int w) //起点，终点，权值 
{
    edge[++cnt].next=head[u];//更新cnt
    edge[cnt].to=v;
    edge[cnt].w=w;
    head[u]=cnt;
}
int main()
{
	int n;
    for(int i=1;i<=n;i++)
    {
    	int a,b,wei;
        addedge(a,b,wei);
        //如果是无向图，还要addedge(b,a,wei);
    }
}

边的遍历

在遍历以x为起点的所有边时，只需要这样就行

for(int i=head[x];i!=0;i=edge[i].next)

这个循环的结束条件是i等于0，因为最后一条边，也就是存边时第一条边，在把head值存进next时，head还没有更新过，也就是0。所以当next返回0时，就说明这些边遍历完毕了。

代码
堆优化

在寻找最短值的时候，用优先队列priority_queue<pair<int,int>>来存储，其中的pair中记录的分别是每条边的权值和终点结点。

优化完成后的总复杂度为O(mlogn)

#include <bits/stdc++.h>
#define rep(i,n,m) for(int i=n;i<=m;++i)
#define per(i,n,m) for(int i=n;i>=m;--i)
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N=250010;
int head[N],ne[N],to[N],w[N],dist[N];
// head记录当前结点连接的最远结点的下标，ne记录当前结点连接的最近结点的下标，
//to记录当前边指向的结点，w记录权值，dist记录目标起点到各个点的最短距离
bool st[N];  //记录当前结点是否已经找到最短距离
int n,m,s,cnt=0;  //cnt是记录每次数据的指针，相当于下标
void addw(int a,int b,int c){
    w[++cnt]=c;
    to[cnt]=b;
    ne[cnt]=head[a];  //更新指向最近结点的下标
    head[a]=cnt;  //更新指向最远结点的下标
}
void Dijkstra()
{
    priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> heap;
    //优先队列自带的排序函数greater，使得默认按第一个元素升序排序
    heap.push({0,s});dist[s]=0;  //s记录的是所求起点，将其放入堆中，距离为0，终点是其自己
    while(!heap.empty()){
        pair<int,int> temp=heap.top();
        heap.pop();     //弹出权值最小的点，待处理
        int x=temp.first,y=temp.second;  
        if(st[y])continue;  //如果该点已经找到最短距离，则跳过
        st[y]=true;  //更新该点已经找到最短距离
        for(int i=head[y];i!=0;i=ne[i]){  //遍历与该点连接的结点
            int t=to[i];    
            if(dist[t]>x+w[i]){  //找到连接的可更新的最短结点
                dist[t]=x+w[i];  //更新权值路径
                heap.push({dist[t],t});  //把该更新过的结点放到堆中待处理
            }
        }
    }
}
int main()
{
    cin>>n>>m;
    memset(dist,INF,sizeof(dist)); //初始化距离无穷大
    for(int i=1;i<=m;++i){
        int a,b,c;cin>>a>>b>>c;
        addw(a,b,c);
    }
    Dijkstra();
    rep(i,1,n)cout<<dist[i]<<' ';
    return 0;
}

带负权边问题的spfa算法之后再考虑学不学🙄🙄🙄🙄